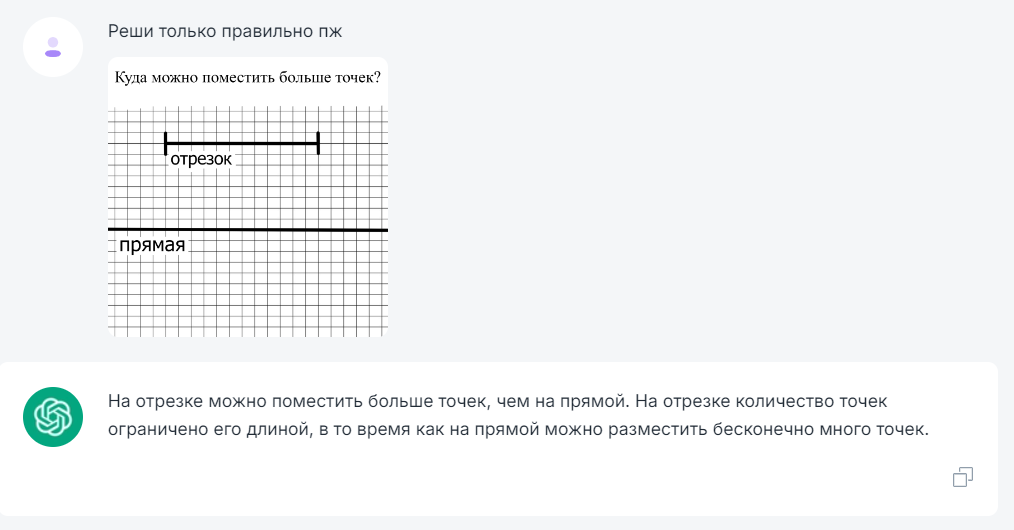
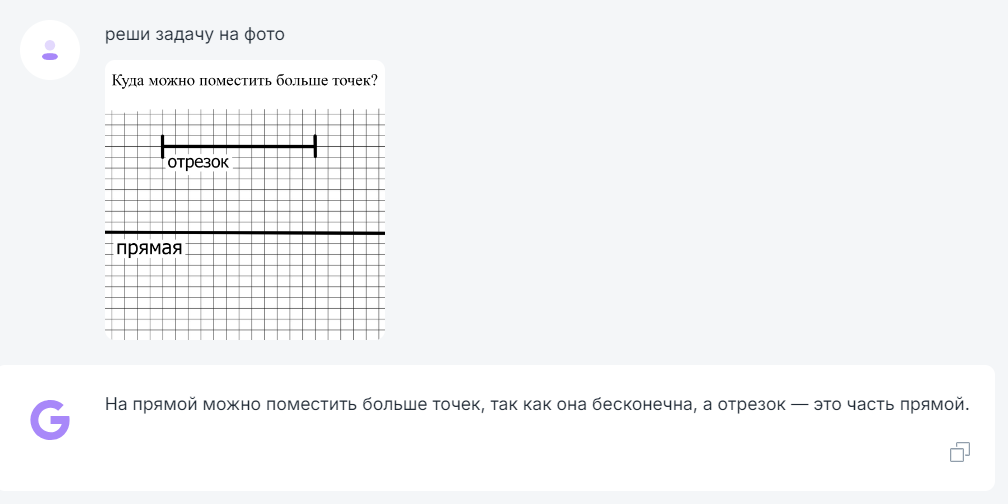
Нейросети в математике: Как искусственный интеллект может решать задачи по геометрии
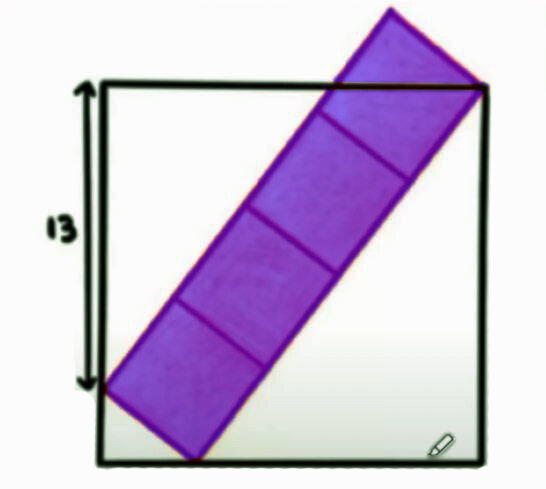
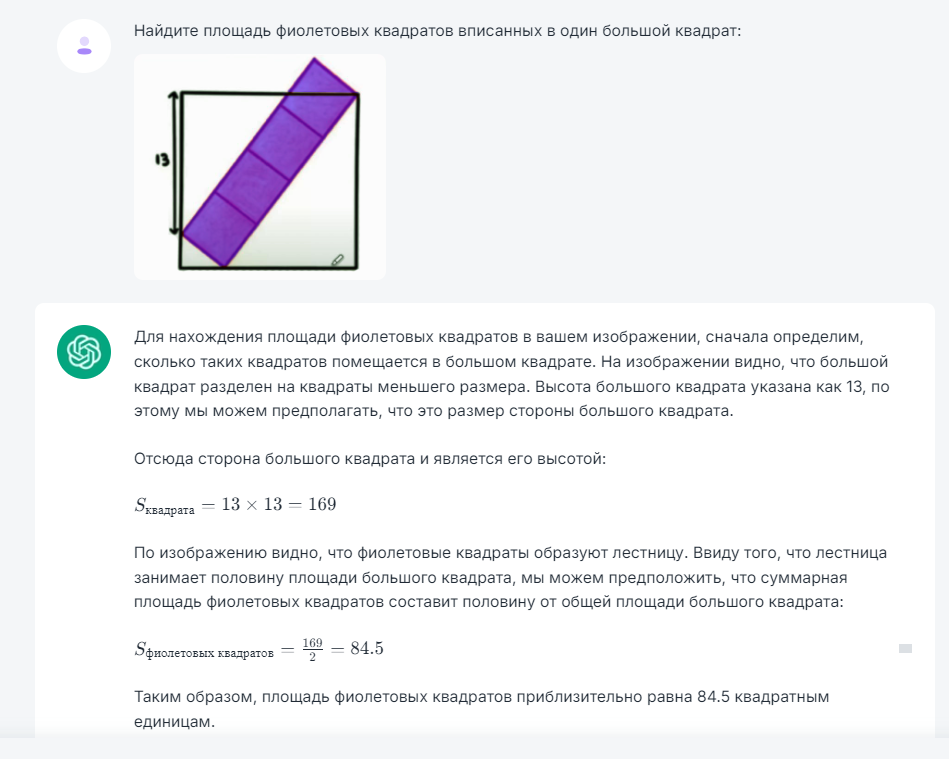
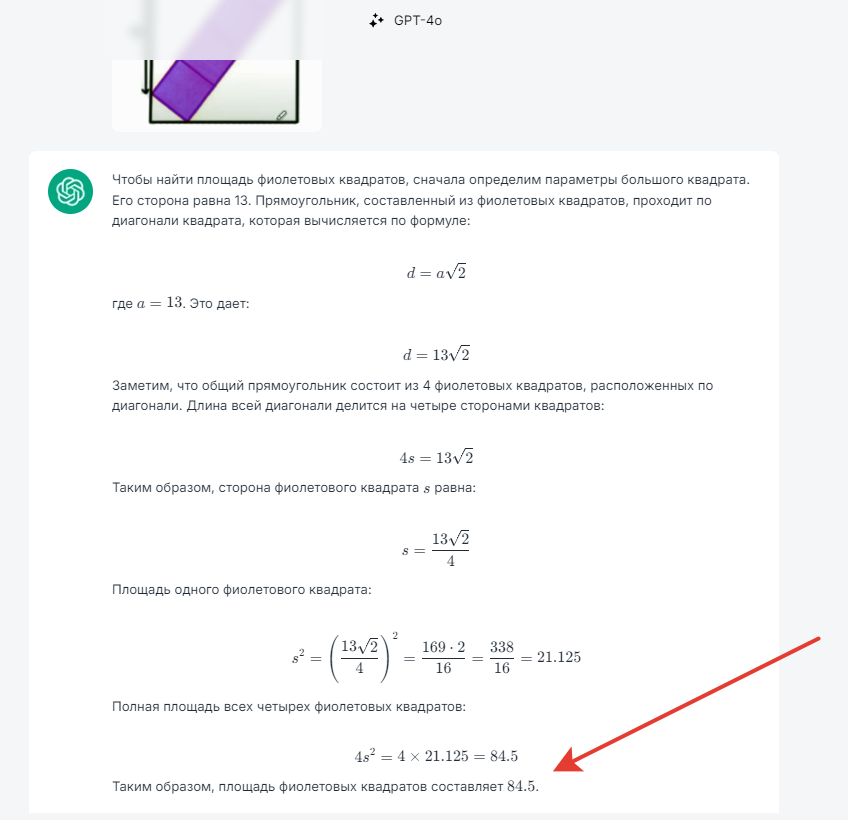
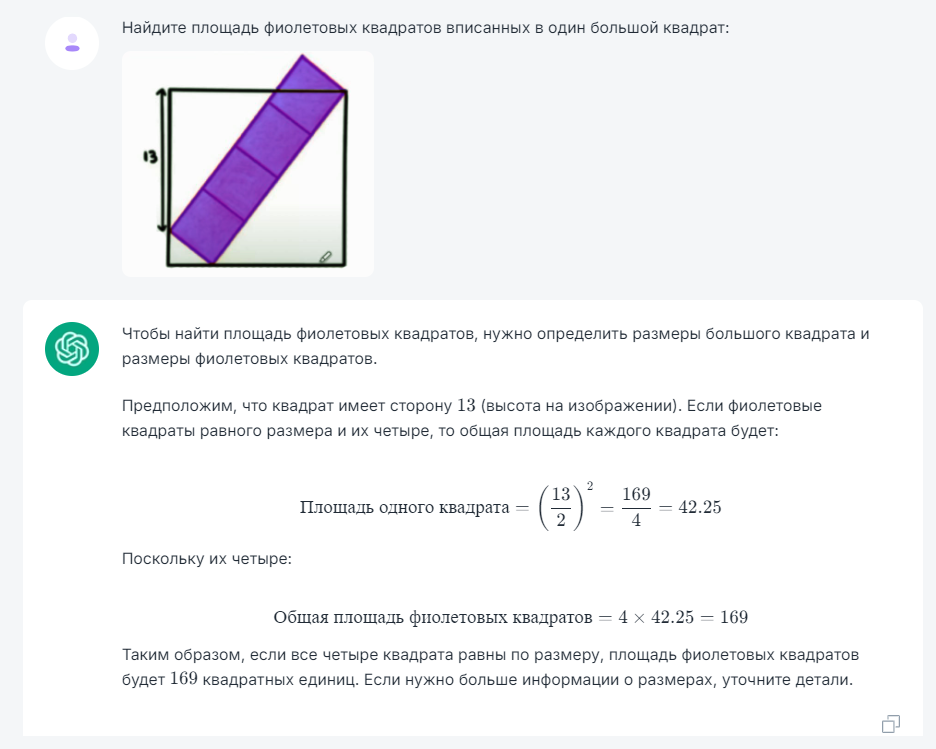
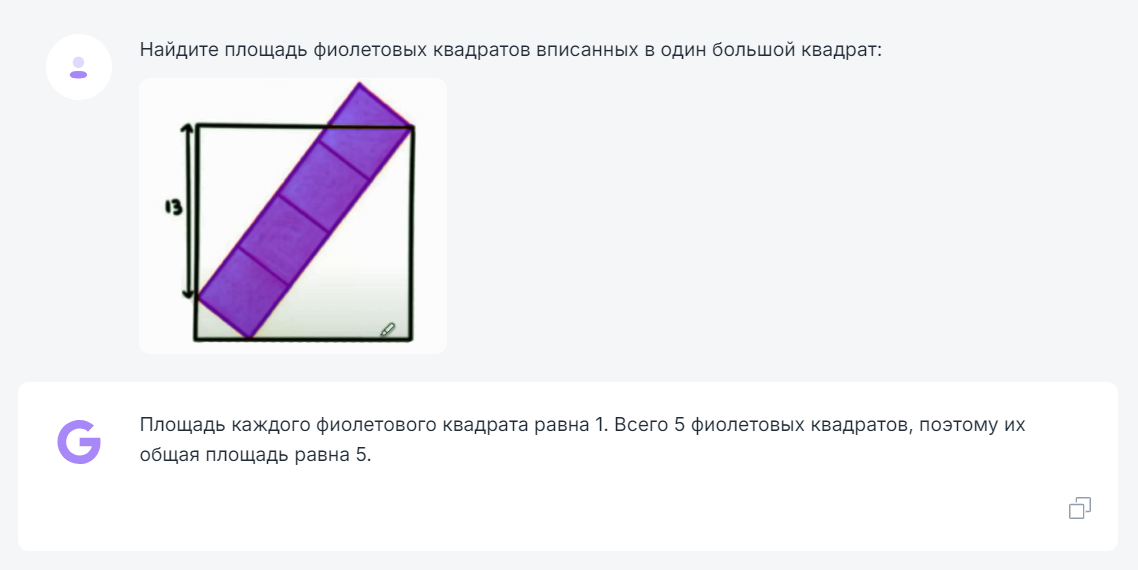
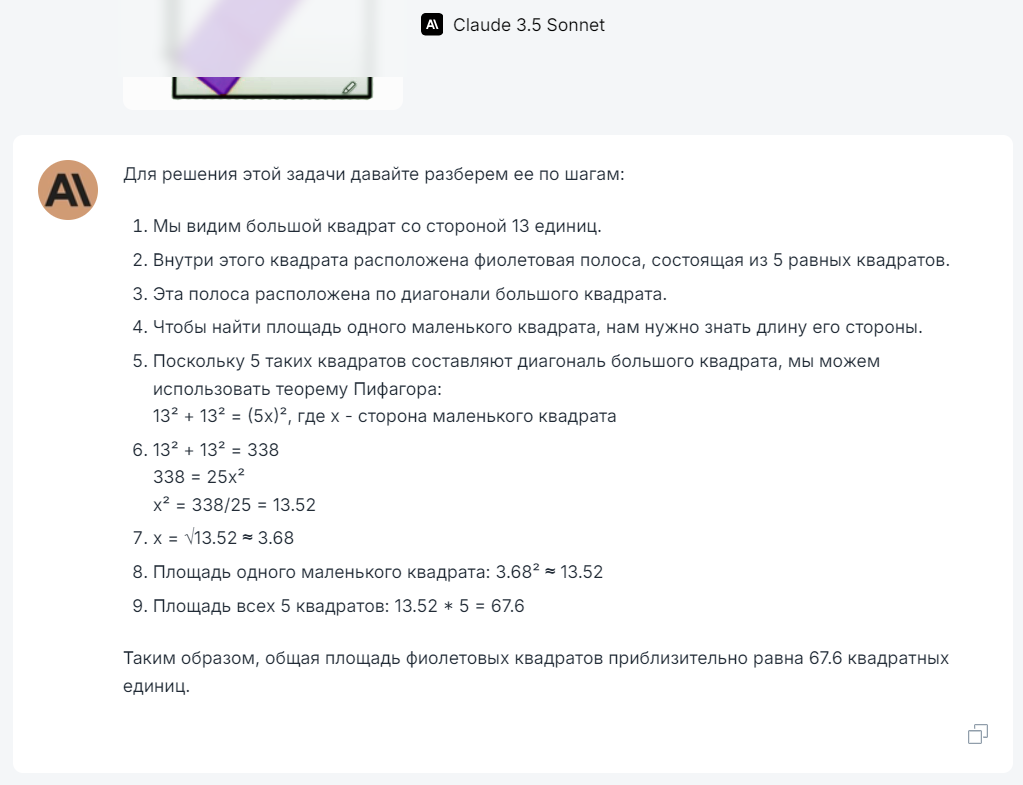
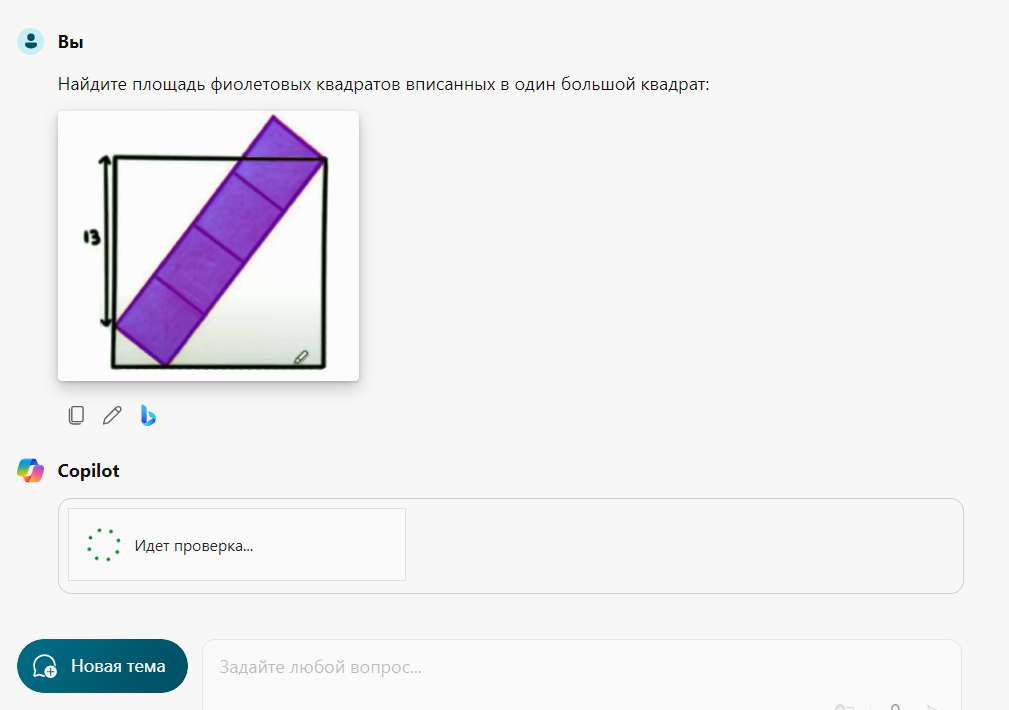
Найдите площадь фиолетовых квадратов вписанных в один большой квадрат:
Всем привет святые роднички) Кто хотел жести в чат gpt?
Кто сможет решить эту загадку не заглядывая в ответы нейронок, тот получит подарок, его имя я в следующем посте прикрепляю на доску почета. Не знаю как я буду проверять, но проверю! (100)
А мы с вами попробуем потестить эту задачку с помощью нейросетей! 🔥
Как думаете смогут ли решить следующие нейросети?
ChatGPT 4, версия для решения задач.
Gemini 1.5 (нейросеть от гугла)
Глядя на эту загадку я бы никогда не сказал, что она решает так просто)))
Так красиво все расписал, в корень 169 перевел, но ответ ⛔
Обожаю эти загадки, нейронки лажают ПОСТОЯННО)))) ⛔
Gemini 1.5 (нейросеть от гугла)
Не подведи, слоган этой неросети 😅 Кто помнить прошлые посты поймет
Угараю от его ответов) Где он там нашел 5 фиолетовых квадратов. ⛔⛔
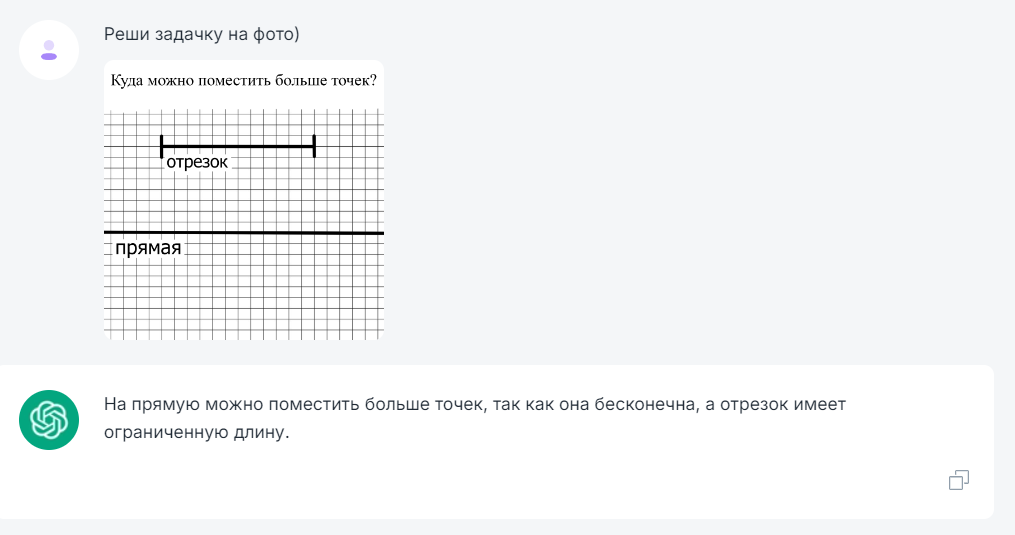
Ребят, у кого копайлот работает? Можете помочь с тестами на нем?) У меня не робит.
НИКТО не на 1 процент не решил эту геометрическую загадку, и в решении задач тут нечего доказывать)
Представим стороны как y - x - z
Углы фиолетовых квадратов 90 градусов, поэтому они равны в местах соприкосновений внизу и на вершине. Z/13 + y - это правая сторона квадрата.
Далее мы выясняем, что сторона y квадрата фиол. равна 3, так как треугольник между квадратом и фиол. квадратами является египетским, если известна одна сторона - 3, то к каждой просто плюсуем 1, в итоге 5 это столона гипотенузы. 5 умножаем на 4 стороны выше = 20 и 5 (это длина гипотенузы) на 20 равно 100)
Если не понятно не проблема. Если понятно можете помочь другим в комментах)